1730: CSP-S21 RMQ 区间最值同题（完善程序）

(RMQ 区何最值同题)给定序列a(0)...a(n-1)，和m次询问，每次詢问给定lr，求
max{a(l)...a(r)}。

为了解决该问題，有一个算法叫 the Method of Four Russians，其时间复杂度为
O(n+m)，步聚如下：
• 建立Cartesian(笛卡尔)树，将问题转化为树上的LCA(最近公共祖先)问题。
• 对于LCA 问题，可以考虑其 Euler 序(即按照 DFS 过程，经过所有点，环游回根的序列)，即求 Euler 序列上两点间一个新的 RMQ 问题。
• 注意新的问题为 士1RMQ，即相邻两点的深度差一定为1。

下面解决这个 士1RMQ 问题，“序列”指 Euler 序列：
•设t为Euler序列长度。取b=ceil(log2(t)/2)。将序列每b个分为一大块，使用ST表(倍增表)处理大块间的RMQ问题，复杂度O(t/b*log(t))=O(n)。
•(重点)对于一个块内的RMQ问题，也需要O(1)的算法。由于差分数组2^(b-1)种，可以预处理出所有情况下的最值位置，预处理复杂度O(b*2^b)，不超过O(n)。
•最终，对于一个查询，可以转化为中间整的大块的 RMQ 问题，以及两端块内的 RMQ问题。

试补全程序。

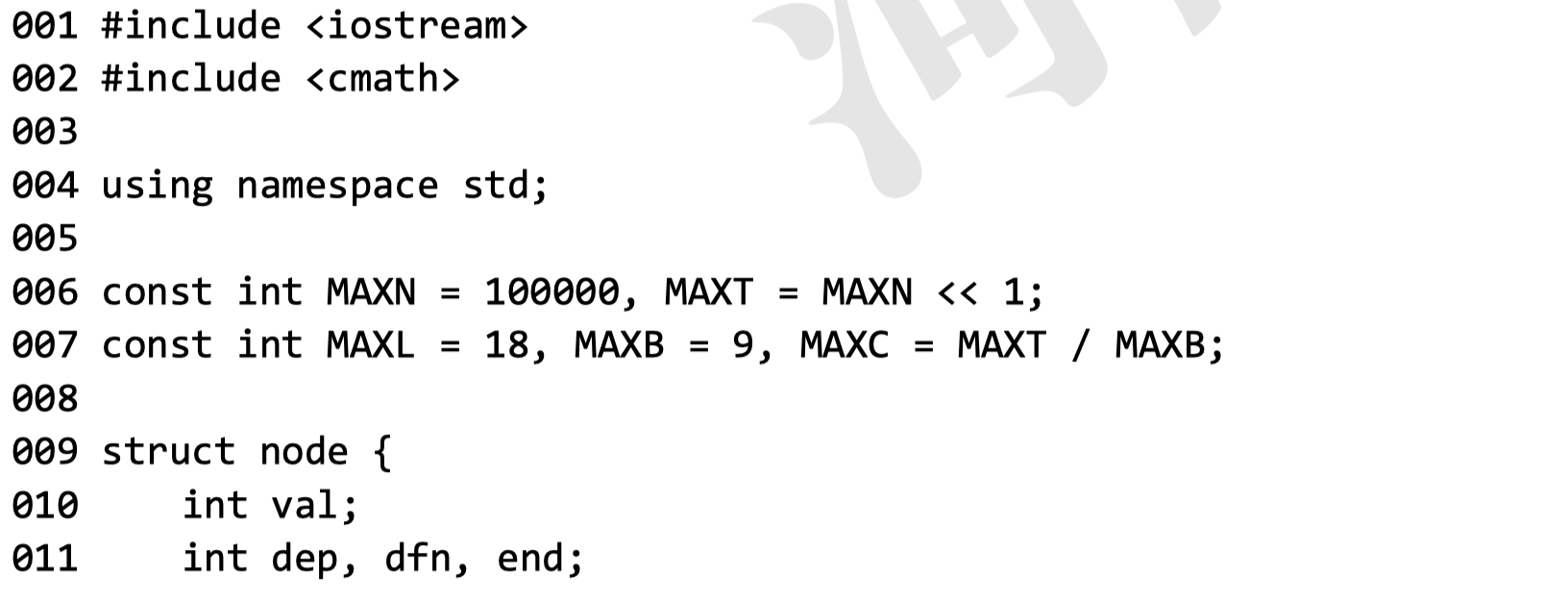
1. ①处应填（ ）
A. p->son[0] = S[top--]
B. p->son[1] = S[top--]
C. S[top--]->son[0] = p
D. S[top--]->son[1] = p

2. ②处应填（ ）
A. p->son[0] = S[top]
B. p->son[1] = S[top]
C. S[top]->son[0] = p
D. S[top]->son[1] = p

3. ③处应填（ ）
A. x->dep < y->dep
B. x < y
C. x->dep > y->dep
D. x->val < y->val

4. ④处应填（ ）
A. A[i * b + j - 1] == A[i * b + j]->son[0]
B. A[i * b + j]->val < A[i * b + j - 1]->val
C. A[i * b + j] == A[i * b + j - 1]->son[1]
D. A[i * b + j]->dep < A[i * b + j - 1]->dep

5. ⑤处应填（ ）
A. v += (S >> i & 1) ? -1 : 1
B. v += (S >> i & 1) ? 1 : -1
C. v += (S >> (i - 1) & 1) ? 1 : -1
D. v += (S >> (i - 1) & 1) ? -1 : 1

6. ⑥处应填（ ）
A. (Dif[p] >> (r - p * b)) & ((1 << (r - l)) - 1)
B. Dif[p]
C. (Dif[p] >> (l - p * b)) & ((1 << (r - l)) - 1)
D. (Dif[p] >> ((p + 1) * b - r)) & ((1 << (r - l + 1)) - 1)